The Accessor Protocol

In this post, I'll introduce you to the accessor protocol for generalized array-like object iteration. First, I'll provide an overview of built-in array-like objects, along with example usage. I'll then show you how you can create your own custom array-like objects using the same element access syntax. Next, we will explore why you might want to go beyond vanilla array-like objects to create more "exotic" variants to accommodate sparsity, deferred computation, and performance considerations. Following this, I'll introduce the accessor protocol and how it compares to possible alternatives. Finally, I'll showcase various example applications.

Sound good?! Great! Let's go!

TL;DR

The accessor protocol (also known as the get/set protocol) defines a standardized way for non-indexed collections to access element values. In order to be accessor protocol-compliant, an array-like object must implement two methods having the following signatures:

function get<T>( index: number ): T {...}
function set<T, U>( value: T, index: number ): U {...}

The protocol allows implementation-dependent behavior when an index is out-of-bounds and, similar to built-in array bracket notation, only requires that implementations support nonnegative index values. In short, the protocol prescribes a minimal set of behavior in order to support the widest possible set of use cases, including, but not limited to, sparse arrays, arrays supporting "lazy" (or deferred) materialization, shared memory views, and arrays which clamp, wrap, or constrain index values.

The following code sample provides an example class returning an array-like object implementing the accessor protocol and supporting strided access over a linear data buffer.

/**
* Class defining a strided array.
*/
class StridedArray {
    // Define private instance fields:
    #length; // array length
    #data;   // underlying data buffer
    #stride; // step size (i.e., the index increment between successive values)
    #offset; // index of the first indexed value in the data buffer

    /**
    * Returns a new StridedArray instance.
    *
    * @param {integer} N - number of indexed elements
    * @param {ArrayLikeObject} data - underlying data buffer
    * @param {number} stride - step size
    * @param {number} offset - index of the first indexed value in the data buffer
    * @returns {StridedArray} strided array instance
    */
    constructor( N, data, stride, offset ) {
        this.#length = N;
        this.#data = data;
        this.#stride = stride;
        this.#offset = offset;
    }

    /**
    * Returns the array length.
    *
    * @returns {number} array length
    */
    get length() {
        return this.#length;
    }

    /**
    * Returns the element located at a specified index.
    *
    * @param {number} index - element index
    * @returns {(void|*)} element value
    */
    get( index ) {
        return this.#data[ this.#offset + index*this.#stride ];
    }

    /**
    * Sets the value for an element located at a specified index.
    *
    * @param {*} value - value to set
    * @param {number} index - element index
    */
    set( value, index ) {
        this.#data[ this.#offset + index*this.#stride ] = value;
    }
}

// Define a data buffer:
const buf = new Float64Array( [ 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0 ] );

// Create a strided view over the data buffer:
const x1 = new StridedArray( 4, buf, 2, 1 );

// Retrieve the second element:
const v1 = x1.get( 1 );
// returns 4.0

// Mutate the second element:
x1.set( v1*10.0, 1 );

// Retrieve the second element:
const v2 = x1.get( 1 );
// returns 40.0

// Create a new strided view over the same data buffer, but reverse the elements:
const x2 = new StridedArray( 4, buf, -2, buf.length-1 );

// Retrieve the second element:
const v3 = x2.get( 1 );
// returns 6.0

// Mutate the second element:
x2.set( v3*10.0, 1 );

// Retrieve the second element:
const v4 = x2.get( 1 );
// returns 60.0

// Retrieve the third element from the first array view:
const v5 = x1.get( 2 );
// returns 60.0

As shown in the code sample above, a strided array is a powerful abstraction over built-in arrays and typed arrays, as it allows for arbitrary views having custom access patterns over a single buffer. In fact, strided arrays are the conceptual basis for multi-dimensional arrays, such as NumPy's ndarray and stdlib's ndarray, which are the fundamental building blocks of modern numerical computing. Needless to say, the example above speaks to the utility of going beyond built-in bracket syntax and providing APIs for generalized array-like object iteration.

To learn more about the accessor protocol and its use cases, continue reading the rest of the post below! 🚀

stdlib

A brief overview about stdlib. stdlib is a standard library for numerical and scientific computation for use in web browsers and in server-side runtimes supporting JavaScript. The library provides high-performance and rigorously tested APIs for data manipulation and transformation, mathematics, statistics, linear algebra, pseudorandom number generation, array programming, and a whole lot more.

We're on a mission to make JavaScript (and TypeScript!) a preferred language for numerical computation. If this sounds interesting to you, check out the project on GitHub, and be sure to give us a star 🌟!

Introduction

In JavaScript, we use bracket notation to access individual array elements. For example, in the following code sample, we use bracket notation to retrieve the second element in an array.

const x = [ 1, 2, 3 ];

// Retrieve the second element:
const v = x[ 1 ];
// returns 2

This works for both generic array and typed array instances. In the next code sample, we repeat the previous operation on a typed array.

const x = new Float64Array( [ 1, 2, 3 ] );
// returns <Float64Array>

// Retrieve the second element:
const v = x[ 1 ];
// returns 2

Similarly, one can use bracket notation for built-in array like objects, such as strings. In the next code sample, we retrieve the second UTF-16 code unit in a string.

const s = 'beep boop';

// Retrieve the second UTF-16 code unit:
const v = s[ 1 ];
// returns 'e'

In order to determine how many elements are in an array-like object, we can use the length property, as shown in the following code sample.

const x = [ 1, 2, 3 ];

const len = x.length;
// returns 3

Arrays and typed arrays are referred to as indexed collections, where elements are ordered according to their index value. An array-like object is thus an ordered list of values that one refers to using a variable name and index.

While JavaScript arrays and typed arrays have many methods (e.g., forEach, map, filter, sort, and more), the only required property that any array-like object (built-in or custom) must have is a length property. The length property tells us the maximum number of elements for which we can apply an operation. Without it, we'd never know when to stop iterating in a for loop!

Custom array-Like objects

We can create our own custom array-like objects using vanilla object literals. For example, in the following code sample, we create an object having numbered keys and a length property and retrieve the value associated with the key 1 (i.e., the second element).

const x = {
    'length': 3,
    '0': 1,
    '1': 2,
    '2': 3
};

// Retrieve the second element:
const v = x[ 1 ];
// returns 2

Notice that we're able to use numeric "indices". This is because, per the ECMAScript Standard, any non-symbol value used as a key is first converted to a string before performing property-value look-up. In which case, so long as downstream consumers don't assume the existence of specialized methods, but stick to only indexed iteration, downstream consumers can adopt array-like object neutrality.

For example, suppose we want to compute the sum of all elements in an array-like object. We could define the following function which accepts, as its sole argument, any object having a length property and supporting value access via numeric indices.

function sum( x ) {
    let total = 0;
    for ( let i = 0; i < x.length; i++ ) {
        total += x[ i ];
    }
    return total;
}

We can then provide all manner of array-like objects and sum is none-the-wiser, being capable of handling them all. In the following code sample, we separately provide a generic array, a typed array, and an array-like object, and, for each input value, the sum function readily computes the sum of all elements.

const x1 = [ 1, 2, 3 ];
const s1 = sum( x1 );
// returns 6

const x2 = new Int32Array( [ 1, 2, 3 ] );
const s2 = sum( x2 );
// returns 6

const x3 = {
    'length': 3,
    '0': 1,
    '1': 2,
    '2': 3
};
const s3 = sum( x3 );
// returns 6

This is great! So long as downstream consumers make minimal assumptions regarding the existence of prototype methods, preferably avoiding the use of methods entirely, we can create functional APIs capable of operating on any indexed collection.

But wait, what about those scenarios in which we want to use alternative data structures, such that property-value pairs are not so neatly aligned, or we want to leverage deferred computation, or create views on existing array-like objects? How can we handle those use cases?

Motivating use cases

Sparse arrays

Up until this point, we've concerned ourselves with "dense" arrays (i.e., arrays in which all elements can be stored sequentially in a contiguous block of memory). In JavaScript, in addition to dense arrays, we have the concept of "sparse" arrays. The following code sample demonstrates sparse array creation by setting an element located at an index which vastly exceeds the length of the target array.

const x = [];

// Convert `x` into a sparse array:
x[ 10000 ] = 3.14;

// Retrieve the second element:
const v1 = x[ 1 ];
// returns undefined

// Retrieve the last element:
const v10000 = x[ 10000 ];
// returns 3.14

// Retrieve the number of elements:
const len = x.length;
// returns 10001

Suffice it to say that, by not using the Array.prototype.push method and filling in values until element 10000, JavaScript engines responsible for compiling and optimizing your code treat the array as if it were a normal object, which is a reasonable optimization in order to avoid unnecessary memory allocation. Creating a sparse array in this fashion is often referred to as converting an array into "dictionary-mode", where an array is stored in a manner similar to a regular object instance. The above code sample is effectively equivalent to the following code sample where we explicitly define x to be an array-like object containing a single defined value at index 10000.

const x = {
    'length': 10001,
    '10000': 3.14
};

// Retrieve the second element:
const v1 = x[ 1 ];
// returns undefined

// Retrieve the last element:
const v10000 = x[ 10000 ];
// returns 3.14

Creating sparse arrays in this manner is fine for many use cases, but less than optimal in others. For example, in numerical computing, we'd prefer that the "holes" (i.e., undefined values) in our sparse array would be 0, rather than undefined. This way, the sum function we defined above could work on both sparse and dense arrays alike (setting aside, for the moment, any performance considerations).

Deferred computation

Next up, consider the case in which we want to avoid materializing array values until they are actually needed. For example, in the following snippet, we'd like the ability to define an array-like object without any pre-defined values and which supports "lazy" materialization such that values are materialized upon element access.

const x = {
    'length': 3
};

// Materialize the first element:
const v0 = x[ 0 ];
// returns 1

// Materialize the second element:
const v1 = x[ 1 ];
// returns 2

// Materialize the third element:
const v2 = x[ 2 ];
// returns 3

To implement lazy materialization in JavaScript, we could utilize the Iterator protocol; however, iterators are not directly "indexable" in a manner similar to array-like objects, and they don't generally have a length property indicating how many elements they contain. To know when they finish, we need to explicitly check the done property of the iterated value. While we can use the built-in for...of statement to iterate over Iterables, this requires either updating our sum implementation to use for...of, and thus require that all provided array-like objects also be Iterables, or introducing branching logic based on the type of value provided. Neither option is ideal, with both entailing increased complexity, constraints, performance-costs, or, more likely, some combination of the above.

Shared memory views

For our next motivating example, consider the case of creating arbitrary views over the same underlying block of memory. While typed arrays support creating contiguous views (e.g., by providing a shared ArrayBuffer to typed array constructors), situations may arise where we want to define non-contiguous views. In order to avoid unnecessary memory allocation, we'd like the ability to define arbitrary iteration patterns which allow accessing particular elements within an underlying linear data buffer.

In the following snippet, we illustrate the use case of an array-like object containing complex numbers which are stored in memory as interleaved real and imaginary components. To allow accessing and manipulating just the real components within the array, we'd like the ability to create a "view" atop the underlying data buffer which accesses every other element (i.e., just the real components). We could similarly create a "view" for only accessing the imaginary components.

// Define a data buffer of interleaved real and imaginary components:
const buf = [ 1.0, -2.0, 3.0, -4.0, 5.0, -6.0, 7.0, -8.0 ];

// Create a complex number array:
const x = new ComplexArray( buf );

// Retrieve the second element:
const z1 = x[ 1 ];
// returns Complex<3.0, -4.0>

// Create a view which only accesses real components:
const re = x.reals();

// Retrieve the real component of the second complex number:
const r = re[ 1 ];
// returns 3.0

// Mutate the real component:
re[ 1 ] = 10.0;

// Retrieve the second element of the complex number array:
const z2 = x[ 1 ];
// returns Complex<10.0, -4.0>

To implement such views, we'd need three pieces of information: (1) an underlying data buffer, (2) an array stride which defines the number of locations in memory between successive array elements, and (3) an offset which defines the location in memory of the first indexed element. For contiguous arrays, the array stride is unity, and the offset is zero. In the example above, for a real component view, the array stride is two, and the offset is zero; for an imaginary component view, the array stride is also two, but the offset is unity. Ideally, we could define a means for providing generalized access such that array-like objects which provide abstracted element indexing can also be provided to array-agnostic APIs, such as sum above.

Backing data structures

As a final example, consider the case where we'd like to compactly store an ordered sequence of boolean values. While we could use generic arrays (e.g., [true,false,...,true]) or Uint8Array typed arrays for this, doing so would not be the most memory efficient approach. Instead, a more memory efficient data structure would be a bit array comprised of a sequence of integer words in which, for each word of n bits, a 1-bit indicates a value of true and a 0-bit indicates a value of false.

The following code snippet provides a general idea of mapping a sequence of boolean values to bits, along with desired operations for setting and retrieving boolean elements.

const seq = [ true, false, true, ..., false, true, false ];
// bit array:    1      0     1  ...      0     1      0    => 101...010

const x = new BooleanBitArray( seq );

// Retrieve the first element:
const v0 = x[ 0 ];
// returns true

// Retrieve the second element:
const v1 = x[ 1 ];
// returns false

// Retrieve the third element:
const v2 = x[ 2 ];
// returns true

// Set the second element:
x[ 1 ] = true;

// Retrieve the second element:
const v3 = x[ 1 ];
// returns true

In JavaScript, we could attempt to subclass array or typed array built-ins in order to allow setting and getting elements via bracket notation; however, this approach would prove limiting as subclassing alone does not allow intercepting property access (e.g., x[i]), which would be needed in order to map an index to a specific bit. We could try and combine subclassing with Proxy objects, but this would come with a steep performance cost due to property accessor indirection--something which we'll revisit later in this post.

Accessor Protocol

To accommodate the above use cases and more, we'd like to introduce a conceptually simple, but very powerful, new protocol: the accessor protocol for generalized element access and iteration of array-like objects. The protocol doesn't require new syntax or built-ins. The protocol only defines a standard way to get and set element values.

Any array-like object can implement the accessor protocol (also known as the get/set protocol) by following two conventions.

1. Define a get method. A get method accepts a single argument: an integer value specifying the index of the element to return. Similar to bracket notation for built-in array and typed array objects, the protocol requires that the get method be defined for integer values that are nonnegative and within array bounds. Protocol-compliant implementations may choose to support negative index values, but that behavior should not be considered portable. Similarly, how implementations choose to handle out-of-bounds indices is implementation-dependent; implementations may return undefined, raise an exception, wrap, clamp, or some other behavior. By not placing restrictions on out-of-bounds behavior, the protocol can more readily accommodate a broader set of use cases.
2. Define a set method. A set method accepts two arguments: the value to set and an integer value specifying the index of the element to replace. Similar to the get method, the protocol requires that the set method be defined for integer indices that are nonnegative and within array bounds. And similarly, protocol-compliant implementations may choose to support negative index values, but that behavior should not be considered portable, and how implementations choose to handle out-of-bounds indices is implementation-dependent.

The following code sample demonstrates an accessor protocol-compliant array-like object.

// Define a data buffer:
const data = [ 1, 2, 3, 4, 5 ];

// Define a minimal array-like object supporting the accessor protocol:
const x = {
    'length': 5,
    'get': ( index ) => data[ index ],
    'set': ( value, index ) => data[ index ] = value
};

// Retrieve the third element:
const v1 = x.get( 2 );
// returns 3

// Set the third element:
x.set( 10, 2 );

// Retrieve the third element:
const v2 = x.get( 2 );
// returns 10

Three things to note about the above code sample.

1. The above example demonstrates another potential use case—namely, an array-like object which doesn't own the underlying data buffer and, instead, acts as a proxy for element access requests.
2. The signature for the set method may seem counter-intuitive, as one might expect the arguments to be reversed. The rationale for value being the first argument and index being the second argument is to be consistent with built-in typed array set method conventions, where the first argument is an array from which to copy values and the second argument is optional and specifies the offset at which to begin writing values from the first argument. While one could argue that set(v,i) is not ideal, given the argument order precedent found in built-ins, the protocol follows that precedent in order to avoid confusion.
3. In contrast to the built-in typed array set method which expects an array (or typed array) for the first argument, the accessor protocol only requires that protocol-compliant implementations support a single element value. Protocol-compliant implementations may choose to support first arguments which are array-like objects and do so in a manner emulating arrays and typed arrays; however, such behavior should not be considered portable.

In short, in order to be accessor protocol-compliant, an array-like object only needs to support single element retrieval and mutation via dedicated get and set methods, respectively.

While built-in typed arrays provide a set method, they are not accessor protocol-compliant, as they lack a dedicated get method, and built-in arrays are also not accessor protocol-compliant, as they lack both a get and a set method. Their lack of compliance is expected and, from the perspective of the protocol, by design in order to distinguish indexed collections from accessor protocol-compliant array-like objects.

Array-like objects implementing the accessor protocol should be expected to pay a small, but likely non-negligible, performance penalty relative to indexed collections using bracket notation for element access. As such, we expect that performance-conscious array-agnostic APIs will maintain two separate code paths: one for indexed collections and one for collections implementing the accessor protocol. Hence, the presence or absence of get and set methods provides a useful heuristic for determining which path takes priority. In general, for indexed collections which are also accessor protocol-compliant, the get and set methods should always take precedent over bracket notation.

The following code sample refactors the sum API defined above to accommodate array-like objects supporting the accessor protocol.

function isAccessorArray( x ) {
    return ( typeof x.get === 'function' && typeof x.set === 'function' );
}

function sum( x ) {
    let total = 0;
    
     // Handle accessor-protocol compliant collections...
    if ( isAccessorArray( x ) ) {
       for ( let i = 0; i < x.length; i++ ) {
            total += x.get( i );
        }
        return total;
    }
    // Handle indexed collections...
    for ( let i = 0; i < x.length; i++ ) {
        total += x[ i ];
    }
    return total;
}

For array-agnostic APIs which prefer brevity over performance optimization, one can refactor the previous code sample to use a small, reusable helper function which abstracts array element access and allows loop consolidation. A demonstration of this refactoring is shown in the following code sample.

function isAccessorArray( x ) {
    return ( typeof x.get === 'function' && typeof x.set === 'function' );
}

function array2accessor( x ) {
    if ( isAccessorArray( x ) ) {
        return x;
    }
    return {
        'length': x.length,
        'get': ( i ) => x[ i ],
        'set': ( v, i ) => x[ i ] = v
    };
}

function sum( x ) {
    let total = 0;
   
    x = array2accessor( x );
    for ( let i = 0; i < x.length; i++ ) {
        total += x.get( i );
    }
    return total;
}

As before, we can then provide all manner of array-like objects, including those supporting the accessor protocol, and sum is none-the-wiser, being capable of handling them all. In the following code sample, we separately provide a generic array, a typed array, an array-like object, and a "lazy" array implementing the accessor protocol, and, for each input value, the sum function readily computes the sum of all elements.

const x1 = [ 1, 2, 3 ];
const s1 = sum( x1 );
// returns 6

const x2 = new Int32Array( [ 1, 2, 3 ] );
const s2 = sum( x2 );
// returns 6

const x3 = {
    'length': 3,
    '0': 1,
    '1': 2,
    '2': 3
};
const s3 = sum( x3 );
// returns 6

const x4 = {
    'length': 3,
    'get': ( i ) => i + 1,
    'set': ( v, i ) => x4[ i ] = v
};
const s4 = sum( x4 );
// returns 6

Alternatives

At this point, you may be thinking that the accessor protocol seems useful, but why invent something new? Doesn't JavaScript already have mechanisms for inheriting indexed collection semantics (subclassing built-ins), supporting lazy materialization (iterators), proxying element access requests (Proxy objects), and accessing elements via a method (Array.prototype.at)?

Yes, JavaScript does have built-in mechanisms for supporting, at least partially, the use cases outlined above; however, each approach has limitations, which I'll discuss below.

Subclassing built-ins

In the early days of the web and prior to built-in subclassing support, third-party libraries would commonly add methods directly to the prototypes of built-in global objects in order to expose functionality missing from the JavaScript standard library—a practice which was, and still remains, frowned upon. After standardization of ECMAScript 2015, JavaScript gained support for subclassing built-ins, including arrays and typed arrays. By subclassing built-ins, we can create specialized indexed collections which not only extend built-in behavior, but also retain the semantics of bracket notation for indexed collections. Subclassing can be particularly beneficial when wanting to augment inherited classes with new properties and methods.

The following code sample demonstrates extending the built-in Array class to support in-place element-wise addition.

/**
* Class which subclasses the built-in Array class.
*/
class SpecialArray extends Array {
    /**
    * Performs in-place element-wise addition.
    *
    * @param {ArrayLikeObject} other - input array
    * @throws {RangeError} must have the same number of elements
    * @returns {SpecialArray} the mutated array
    */
    add( other ) {
        if ( other.length !== this.length ) {
            throw new RangeError( 'Must provide an array having the same length.' );
        }
        for ( let i = 0; i < this.length; i++ ) {
            this[ i ] += other[ i ];
        }
        return this;
    }
}

// Create a new SpecialArray instance:
const x = new SpecialArray( 10 );

// Call an inherited method to fill the array:
x.fill( 5 );

// Retrieve the second element:
const v1 = x[ 1 ];
// returns 5

// Create an array to add:
const y = [ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 ];

// Perform element-wise addition:
x.add( y );

// Retrieve the second element:
const v2 = x[ 1 ];
// returns 7

While powerful, subclassing built-ins has several limitations.

1. With respect to the use cases discussed above, subclassing built-ins only satisfies the desire for preserving built-in bracket notation semantics. Subclassing does not confer support for lazy materialization, separate backing data structures, or shared memory views.
2. Subclassing built-ins imposes a greater implementation burden on subclasses. Particularly for more "exotic" array types, such as read-only arrays, subclasses may be forced to override and re-implement parent methods in order to ensure consistent behavior (e.g., returning a collection having a desired instance type).
3. Subclassing built-ins imposes an ongoing maintenance burden. As the ECMAScript Standard evolves and built-in objects gain additional properties and methods, those properties and methods may need to be overridden and re-implemented in order to preserve desired semantics.
4. Subclassing built-ins influences downstream user expectations. If a subclass inherits from a Float64Array, users will likely expect that any subclass satisfying an instanceof check supports all inherited methods, some of which may not be possible to support (e.g., for a read-only array, methods supporting mutation). Distinct (i.e., non-coupled) classes which explicitly own the interface contract will likely be better positioned to manager user expectations.
5. While subclassing built-ins can encourage reuse, object-oriented programming design patterns can more generally lead to code bloat (read: increased bundle sizes in web applications), as the more methods are added or overridden, the less likely any one of those methods is actually used in a given application.

For the reasons listed above, inheriting from built-ins is generally discouraged in favor of composition due to non-negligible performance and security impacts. One of the principle aims of the accessor protocol is to provide the smallest API surface area necessary in order to facilitate generalized array-like object iteration. Subclassing built-ins is unable to fulfill that mandate.

Iterators

Objects implementing the iterator protocol can readily support deferred computation (i.e., "lazy" materialization), but, for several of the use cases outlined above, the iterator protocol has limited applicability. More broadly, relying on the iterator protocol has three limitations.

First, as alluded to earlier in this post, the iterator protocol does not require that objects have a length property, and, in fact, iterators are allowed to be infinite. As a consequence, for operations requiring fixed memory allocation (e.g., as might be the case when needing to materialize values before passing a typed array from JavaScript to C within a Node.js native add-on), the only way to know how much memory to allocate is by first materializing all iterator values. Doing so may require first filling a temporary array before values can be copied to a final destination. This process is likely to be inefficient.

Furthermore, operations involving multiple iterators can quickly become complex. For example, suppose I want to perform element-wise addition for two iterators X and Y (i.e., x0+y0, x1+y1, ..., xn+yn). This works fine if X and Y have the same "length", but what if they have different lengths? Should iteration stop once one of the iterator ends? Or should a fill value, such as zero, be used? Or maybe this is unexpected behavior, and we should raise an exception? Accordingly, generalized downstream APIs accepting iterators may require tailored options to support various edge cases which simply aren't as applicable when working with array-like objects.

We could, of course, define a protocol requiring that iterators have a length property, but that leads us to the next limitation: iterators do not support random access. In order to access the n-th iterated value, one must materialize the previous n-1 values. This is also likely to be inefficient.

Lastly, in general, code paths operating on iterators are significantly slower than equivalent code paths operating on indexed collections. While the accessor protocol does introduce overhead relative to using bracket notation due to explicitly needing to call a method, the overhead is less than the overhead introduced by iterators.

The following code sample defines three functions: one for computing the sum of an indexed collection, one for computing the sum of an array-like object implementing the accessor protocol, and a third for computing the sum of an iterator using JavaScript's built-in for...of syntax.

function indexedSum( x ) {
    let total = 0;
    for ( let i = 0; i < x.length; i++ ) {
        total += x[ i ];
    }
    return total;
}

function accessorSum( x ) {
    let total = 0;
    for ( let i = 0; i < x.length; i++ ) {
        total += x.get( i );
    }
    return total;
}

function iteratorSum( x ) {
    let total = 0;
    for ( const v of x ) {
        total += v;
    }
    return total;
}

To assess the performance of each function, I ran benchmarks on an Apple M1 Pro running MacOS and Node.js v20.9.0. For a set of array lengths ranging from ten elements to one million elements, I repeated benchmarks three times and used the maximum observed rate for subsequent analysis and chart display. The results are provided in the following grouped column chart.

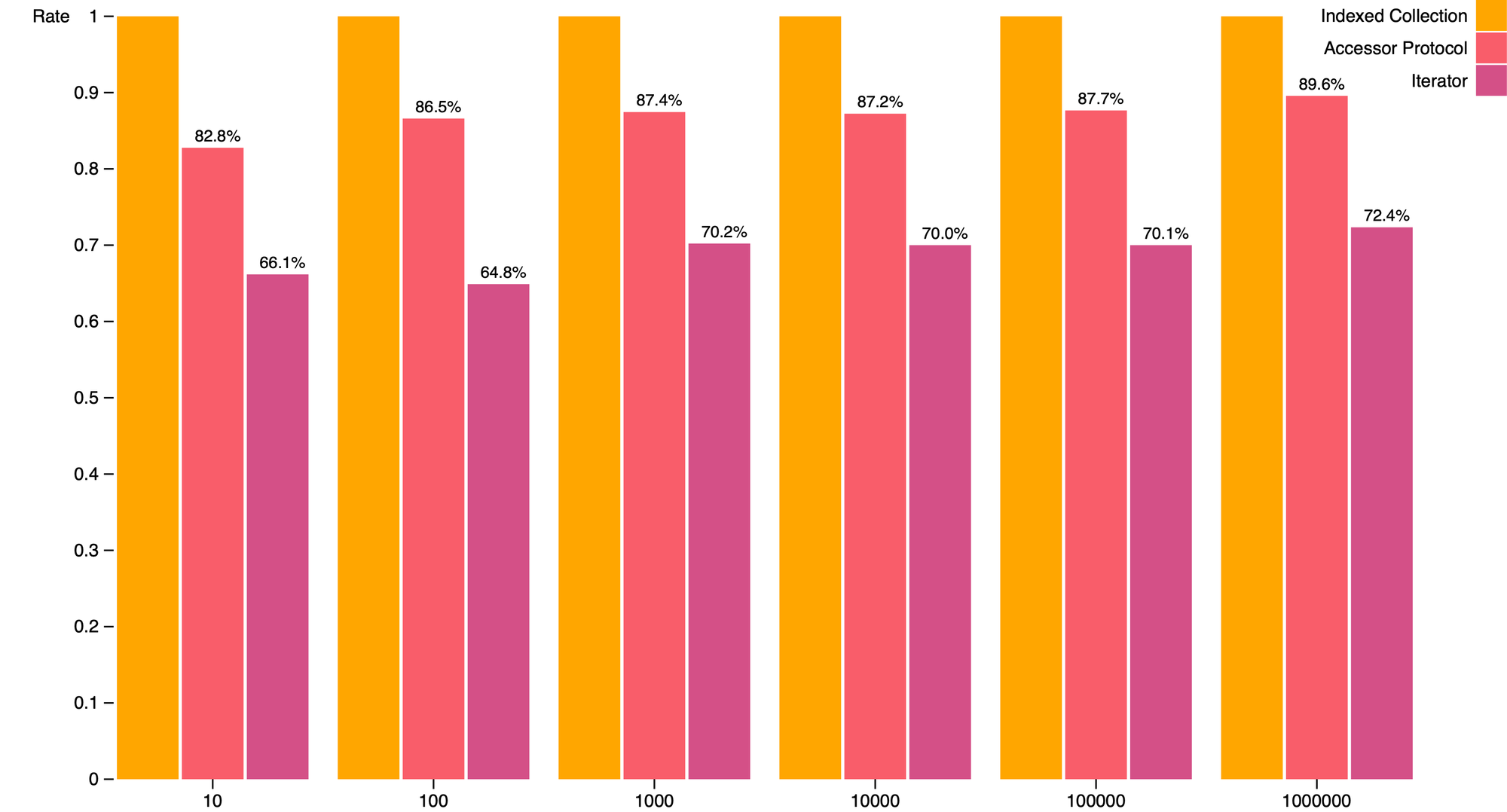
In the chart above, columns along the x-axis are grouped according to input array/iterator length. Accordingly, the first group of columns corresponds to input arrays/iterators having 10 elements, the second group to input array/iterators having 100 elements, and so on and so forth. The y-axis corresponds to normalized rates relative to the performance observed for indexed collections. For example, if the maximum observed rate when summing over an indexed collection was 100 iterations per second and the maximum observed rate when summing over an iterator was 70 iterations per second, the normalized rate is 70/100, or 0.7. Hence, a rate equal to unity indicates an observed rate equal to that of indexed collections. Anything less than unity indicates an observed rate less than that of indexed collections (i.e., summation involving a given input was slower than using built-in bracket notation). Anything greater than unity indicates an observed rate greater than that of indexed collections (i.e., summation involving a given input was faster than using built-in bracket notation).

From the chart, we can observe that, for all array lengths, neither accessor protocol-compliant array-like objects nor iterators matched or exceeded the performance of indexed collections. Array-like objects implementing the accessor protocol were 15% slower than indexed collections, and iterators were 30% slower than indexed collections. These results confirm that the accessor protocol introduces an overhead relative to indexed collections, but not nearly as much as the overhead introduced by iterators.

In short, the accessor protocol is both more flexible and more performant than using iterators.

Computed properties

Another alternative to the accessor protocol is to use defined properties having property accessors. When implementing lazy materialization and proxied element access prior to ECMAScript standardization of Proxy objects and support for Array subclassing, property descriptors were the primary way to emulate the built-in bracket notation of indexed collections.

The following code sample shows an example class returning an array-like object emulating built-in bracket notation by explicitly defining property descriptors for all elements. Each property descriptor defines an accessor property with specialized get and set accessors.

/**
* Class emulating built-in bracket notation for lazy materialization without subclassing.
*/
class LazyArray {
    // Define private instance fields:
    #data; // memoized value cache

    /**
    * Returns a new fixed-length "lazy" array.
    *
    * @param {number} len - number of elements
    * @returns {LazyArray} lazy array instance
    */
    constructor( len ) {
        Object.defineProperty( this, 'length', {
            'configurable': false,
            'enumerable': false,
            'writable': false,
            'value': len
        });
        for ( let i = 0; i < len; i++ ) {
            Object.defineProperty( this, i, {
                'configurable': false,
                'enumerable': true,
                'get': this.#get( i ),
                'set': this.#set( i )
            });
        }
        this.#data = {};
    }

    /**
    * Returns a getter.
    *
    * @private
    * @param {number} index - index
    * @returns {Function} getter
    */
    #get( index ) {
        return get;

        /**
        * Returns an element.
        *
        * @private
        * @returns {*} element
        */
        function get() {
            const v = this.#data[ index ];
            if ( v === void 0 ) {
                // Perform "lazy" materialization:
                this.#data[ index ] = index; // note: toy example
                return index;
            }
            return v;
        }
    }

    /**
    * Returns a setter.
    *
    * @private
    * @param {number} index - index
    * @returns {Function} setter
    */
    #set( index ) {
        return set;

        /**
        * Sets an element value.
        *
        * @private
        * @param {*} value - value to set
        * @returns {boolean} boolean indicating whether a value was set
        */
        function set( value ) {
            this.#data[ index ] = value;
            return true;
        }
    }
}

// Create a new "lazy" array:
const x = new LazyArray( 10 );

// Print the list of elements:
for ( let i = 0; i < x.length; i++ ) {
    console.log( x[ i ] );
}

There are several issues with this approach:

1. Explicitly defining property descriptors is very expensive. Thus, especially for large arrays, instantiation can become prohibitively slow.
2. Creating separate accessors for each property requires significantly more memory than the accessor protocol. The latter only needs two methods to serve all elements. The former requires two methods for every element.
3. Element access is orders of magnitude slower than both built-in bracket notation and the accessor protocol.

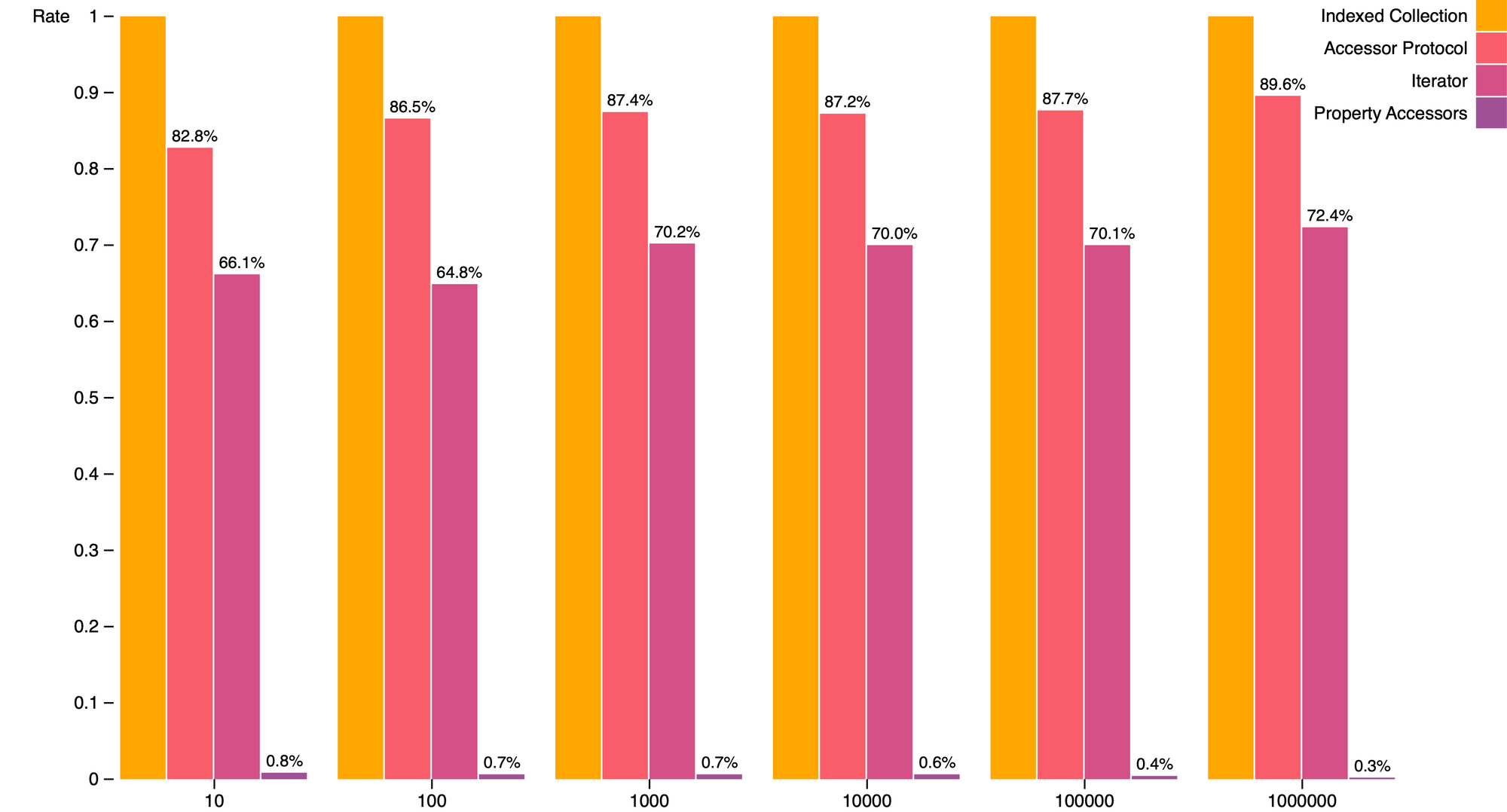
In the following grouped column chart, I show benchmark results for computing the sum over an array-like object which emulates built-in bracket notation by using property accessors. The chart extends the previous grouped column chart by including the same column groups as the previous chart and adding a new column to each group corresponding to property accessor performance results. As can be observed, using property accessors is more than one hundred times slower than either indexed collection built-in bracket notation or the accessor protocol.

Proxies

The Proxy object allows you to create a proxy for another object. During its creation, the proxy can be configured to intercept and redefine fundamental object operations, including getting and setting properties. While proxy objects are commonly used for logging property accesses, validation, formatting, or sanitizing inputs, they enable novel and extremely powerful extensions to built-in behavior. One such extension—implementing Python-like indexing in JavaScript—will be the subject of a future post.

The following code sample defines a function for creating proxied array-like objects which intercept the operations for getting and setting property values. The proxy is created by providing two parameters:

1. target: the original object we want to proxy.
2. handler: an object defining which operations to intercept and how to redefine those operations.

/**
* Tests whether a string contains only integer values.
*
* @param {string} str - input string
* @returns {boolean} boolean indicating whether a string contains only integer values
*/
function isDigitString( str ) {
    return /^\d+$/.test( str );
}

/**
* Returns a proxied array-like object.
*
* @param {number} len - array length
* @returns {Proxy} proxy object
*/
function lazyArray( len ) {
    const target = {
        'length': len
    };
    return new Proxy( target, {
        'get': ( target, property ) => {
            if ( isDigitString( property ) ) {
                return parseInt( property, 10 ); // note: toy example
            }
            return target[ property ];
        },
        'set': ( target, property, value ) => {
            target[ property ] = value;
            return true;
        }
    });
}

// Create a new "lazy" array:
const x = lazyArray( 10 );

// Print the list of elements:
for ( let i = 0; i < x.length; i++ ) {
    console.log( x[ i ] );
}

While proxy objects avoid many of the issues described above for subclassing, iterators, and property accessors, including random access, instantiation costs, and general complexity, their primary limitation at the time of this blog post is performance.

The following group column chart builds on the previous column charts by adding a new column to each group corresponding to proxy object results. As can be observed, using proxy objects fares no better than the property accessor approach described above. Performance is on par with property accessors and more than one hundred times slower than either indexed collection built-in bracket notation or the accessor protocol.

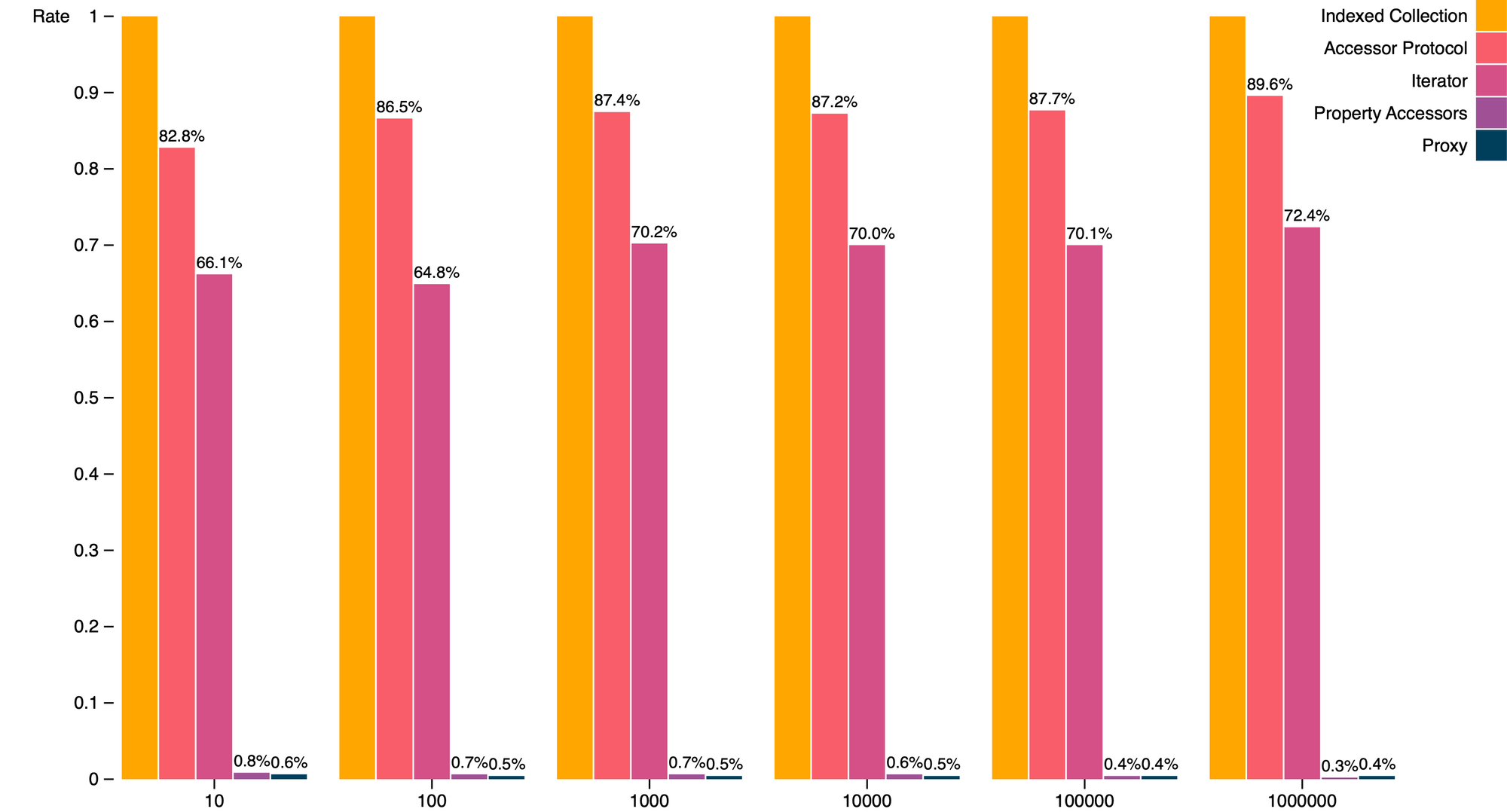
Using "at" rather than "get"

The 2022 revision of the ECMAScript Standard added an at method to array and typed array prototypes which accepts a single integer argument and returns the element at that index, allowing for both positive and negative integers. Why, then, do we need another method for retrieving an array element as proposed in the accessor protocol? This question seems especially salient given that the protocol's get method only requires support for nonnegative integer arguments, making the get method seem less powerful.

There are a few reasons why the accessor protocol chooses to use get, rather than at.

1. The name get has symmetry with the name set.
2. The at method does not have a built-in method equivalent for setting element values. The set method is only present on typed arrays, not generic arrays, and does not support negative target offsets.
3. The at method does not match built-in bracket notation semantics. When using a negative integer within square brackets, the integer value is serialized to a string before property lookup (i.e., x[-1] is equivalent to x['-1']). Unless negative integer properties are explicitly defined, x[-1] will return undefined. In contrast, x.at(-1) is equivalent to x[x.length-1], which, for non-empty arrays, will return the last array element. Accordingly, the get method of the accessor protocol allows protocol-compliant implementations to match built-in bracket notation semantics exactly.
4. The accessor protocol does not specify the behavior of out-of-bounds index arguments. In contrast, when an index argument is negative, the at method normalizes a negative index value according to index + x.length. This, however, is not the only reasonable behavior, depending on the use case. For example, an array-like object implementation may want to clamp out-of-bounds index arguments, such that indices less than zero are clamped to zero (i.e., the first index) and indices greater than x.length-1 are clamped to x.length-1 (i.e., the last index). Alternatively, an array-like object implementation may want to wrap out-of-bounds index arguments using modulo arithmetic. Lastly, an array-like object implementation may want to raise an exception when an index is out-of-bounds. In short, the at method prescribes a particular mode of behavior, which may not be appropriate for all use cases.
5. By only requiring support for nonnegative integer arguments, the accessor protocol allows protocol-compliant implementations to minimize branching and ensure better performance. While convenient, support for negative indices is not necessary for generalized array-like object iteration.
6. As the EMCAScript Standard does not define a get method for arrays and typed arrays (at least not yet!), the presence or absence of a get method in combination with a set method and length property allows for distinguishing indexed collections from array-like objects implementing the accessor protocol. The combination of at, set, and length would not be sufficient for making such a distinction. This ability is important in order to allow downstream array-like object consumers to implement optimized code paths and ensure optimal performance.

For these reasons, an at method is not a suitable candidate for use in generalized array-like object iteration.

Examples

Now that we've considered the alternatives and established the motivation and need for the accessor protocol, what can we do with it?! Glad you asked! To answer this question, I provide several concrete implementations below.

Complex number arrays

Complex numbers have applications in many scientific domains, including signal processing, fluid dynamics, and quantum mechanics. We can extend the concept of typed arrays to the realm of complex numbers by storing real and imaginary components as interleaved values within a real-valued typed array. In the following code sample, I define a minimal immutable complex number constructor and a complex number array class implementing the accessor protocol.

/**
* Class defining a minimal immutable complex number.
*/
class Complex {
    // Define private instance fields:
    #re; // real component
    #im; // imaginary component

    /**
    * Returns a new complex number instance.
    *
    * @param {number} re - real component
    * @param {number} im - imaginary component
    * @returns {Complex} complex number instance
    */
    constructor( re, im ) {
        this.#re = re;
        this.#im = im;
    }

    /**
    * Returns the real component of a complex number.
    *
    * @returns {number} real component
    */
    get re() {
        return this.#re;
    }

    /**
    * Returns the imaginary component of a complex number.
    *
    * @returns {number} imaginary component
    */
    get im() {
        return this.#im;
    }
}

/**
* Class defining a complex number array implementing the accessor protocol.
*/
class Complex128Array {
    // Define private instance fields:
    #length; // array length
    #data;   // underlying data buffer

    /**
    * Returns a new complex number array instance.
    *
    * @param {number} len - array length
    * @returns {Complex128Array} complex array instance
    */
    constructor( len ) {
        this.#length = len;
        this.#data = new Float64Array( len*2 ); // accommodate interleaved components
    }

    /**
    * Returns the array length.
    *
    * @returns {number} array length
    */
    get length() {
        return this.#length;
    }

    /**
    * Returns an array element.
    *
    * @param {integer} index - element index
    * @returns {(Complex|void)} element value
    */
    get( index ) {
        if ( index < 0 || index >= this.#length ) {
            return;
        }
        const ptr = index * 2; // account for interleaved components
        return new Complex( this.#data[ ptr ], this.#data[ ptr+1 ] );
    }

    /**
    * Sets an array element.
    *
    * @param {Complex} value - value to set
    * @param {integer} index - element index
    * @returns {void}
    */
    set( value, index ) {
        if ( index < 0 || index >= this.#length ) {
            return;
        }
        const ptr = index * 2; // account for interleaved components
        this.#data[ ptr ] = value.re;
        this.#data[ ptr+1 ] = value.im;
    }
}

// Create a new complex number array:
const x = new Complex128Array( 10 );
// returns <Complex128Array>

// Retrieve the second element:
const z1 = x.get( 1 );
// returns <Complex>

const re1 = z1.re;
// returns 0.0

const im1 = z1.im;
// returns 0.0

// Set the second element:
x.set( new Complex( 3.0, 4.0 ), 1 );

// Retrieve the second element:
const z2 = x.get( 1 );
// returns <Complex>

const re2 = z2.re;
// returns 3.0

const im2 = z2.im;
// returns 4.0

If you are interested in a concrete implementation of complex number arrays, see the Complex128Array and Complex64Array packages provided by stdlib. We'll have more to say about these packages in future blog posts.

Sparse arrays

Applications of sparse arrays commonly arise in network theory, numerical analysis, natural language processing, and other areas of science and engineering. When data is "sparse" (i.e., most elements are non-zero), sparse array storage can be particularly advantageous in reducing required memory storage and in accelerating the computation of operations involving only non-zero elements.

In the following code sample, I define a minimal accessor protocol-compliant sparse array class using the dictionary of keys (DOK) format and supporting arbitrary fill values. Support for arbitrary fill values is useful as it extends the concept of sparsity to any array having a majority of elements equal to the same value. For such arrays, we can compress an array to a format which stores a single fill value and only those elements which are not equal to the repeated value. This approach is implemented below.

/**
* Class defining a sparse array implementing the accessor protocol.
*/
class SparseArray {
    // Define private instance fields:
    #length; // array length
    #data;   // dictionary containing array elements
    #fill;   // fill value

    /**
    * Returns a new sparse array instance.
    *
    * @param {number} len - array length
    * @param {*} fill - fill value
    * @returns {SparseArray} sparse array instance
    */
    constructor( len, fill ) {
        this.#length = len;
        this.#data = {};
        this.#fill = fill;
    }

    /**
    * Returns the array length.
    *
    * @returns {number} array length
    */
    get length() {
        return this.#length;
    }

    /**
    * Returns an array element.
    *
    * @param {number} index - element index
    * @returns {*} element value
    */
    get( index ) {
        if ( index < 0 || index >= this.#length ) {
            return;
        }
        const v = this.#data[ index ];
        if ( v === void 0 ) {
            return this.#fill;
        }
        return v;
    }

    /**
    * Sets an array element.
    *
    * @param {*} value - value to set
    * @param {number} index - element index
    * @returns {void}
    */
    set( value, index ) {
        if ( index < 0 || index >= this.#length ) {
            return;
        }
        this.#data[ index ] = value;
    }
}

// Create a new sparse array:
const x = new SparseArray( 10, 0.0 );

// Retrieve the second element:
const v1 = x.get( 1 );
// returns 0.0

// Set the second element:
x.set( 4.0, 1 );

// Retrieve the second element:
const v2 = x.get( 1 );
// returns 4.0

Lazy arrays

While less broadly applicable, situations may arise in which you want an array-like object supporting lazy materialization and random access. For example, suppose each element is the result of an expensive computation, and you want to defer the computation of each element until first accessed.

In the following code sample, I define a class supporting lazy materialization of randomly generated element values. When an element is accessed, a class instance eagerly computes all un-computed element values up to and including the accessed element. Once an element value is computed, the value is memoized and can only be overridden by explicitly setting the element.

/**
* Class defining an array-like object supporting lazy materialization of random values.
*/
class LazyRandomArray {
    // Define private instance fields:
    #data;   // underlying data buffer

    /**
    * Returns a new lazy random array.
    *
    * @returns {LazyRandomArray} new instance
    */
    constructor() {
        this.#data = [];
    }

    /**
    * Materializes array elements.
    *
    * @private
    * @param {number} len - array length
    */
    #materialize( len ) {
        for ( let i = this.#data.length; i < len; i++ ) {
            this.#data.push( Math.random() );
        }
    }

    /**
    * Returns the array length.
    *
    * @returns {number} array length
    */
    get length() {
        return this.#data.length;
    }

    /**
    * Returns an array element.
    *
    * @param {number} index - element index
    * @returns {*} element value
    */
    get( index ) {
        if ( index < 0 ) {
            return;
        }
        if ( index >= this.#data.length ) {
            this.#materialize( index+1 );
        }
        return this.#data[ index ];
    }

    /**
    * Sets an array element.
    *
    * @param {*} value - value to set
    * @param {number} index - element index
    * @returns {void}
    */
    set( value, index ) {
        if ( index < 0 ) {
            return;
        }
        if ( index >= this.#data.length ) {
            // Materialize `index+1` in order to ensure "fast" elements:
            this.#materialize( index+1 );
        }
        this.#data[ index ] = value;
    }
}

// Create a new lazy array:
const x = new LazyRandomArray();

// Retrieve the tenth element:
const v1 = x.get( 9 );
// returns <number>

// Set the tenth element:
x.set( 4.0, 9 );

// Retrieve the tenth element:
const v2 = x.get( 9 );
// returns 4.0

// Return the number of elements in the array:
const len = x.length;
// returns 10

stdlib

While array-like objects implementing the accessor protocol are useful in their own right, they become all the more powerful when combined with functional APIs which are accessor protocol-aware. Fortunately, stdlib treats accessor protocol-compliant objects as first-class citizens, providing support for them throughout its codebase.

For example, the following code sample uses @stdlib/array-put to replace the elements of an accessor protocol-compliant strided array at specified indices.

const put = require( '@stdlib/array-put' );

/**
* Class defining a strided array.
*/
class StridedArray {
    // Define private instance fields:
    #length; // array length
    #data;   // underlying data buffer
    #stride; // step size (i.e., the index increment between successive values)
    #offset; // index of the first indexed value in the data buffer

    /**
    * Returns a new StridedArray instance.
    *
    * @param {integer} N - number of indexed elements
    * @param {ArrayLikeObject} data - underlying data buffer
    * @param {number} stride - step size
    * @param {number} offset - index of the first indexed value in the data buffer
    * @returns {StridedArray} strided array instance
    */
    constructor( N, data, stride, offset ) {
        this.#length = N;
        this.#data = data;
        this.#stride = stride;
        this.#offset = offset;
    }

    /**
    * Returns the array length.
    *
    * @returns {number} array length
    */
    get length() {
        return this.#length;
    }

    /**
    * Returns the element located at a specified index.
    *
    * @param {number} index - element index
    * @returns {(void|*)} element value
    */
    get( index ) {
        return this.#data[ this.#offset + index*this.#stride ];
    }

    /**
    * Sets the value for an element located at a specified index.
    *
    * @param {*} value - value to set
    * @param {number} index - element index
    */
    set( value, index ) {
        this.#data[ this.#offset + index*this.#stride ] = value;
    }
}

// Define a data buffer:
const buf = new Float64Array( [ 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0 ] );

// Create a strided view over the data buffer:
const x1 = new StridedArray( 4, buf, 2, 1 );

// Retrieve the second element:
const v1 = x1.get( 1 );
// returns 4.0

// Retrieve the fourth element:
const v2 = x1.get( 3 );
// returns 8.0

// Replace the second and fourth elements with new values:
put( x, [ 1, 3 ], [ -v1, -v2 ] );

// Retrieve the second element:
const v3 = x1.get( 1 );
// returns -4.0

// Retrieve the fourth element:
const v4 = x1.get( 3 );
// returns -8.0

In addition to supporting accessor protocol-compliant array-like objects in utilities, linear algebra operations, and other vectorized APIs, stdlib has leveraged the accessor protocol to implement typed arrays supporting data types beyond real-valued numbers. To see this in action, see stdlib's Complex128Array, Complex64Array, and BooleanArray typed array constructors.

In short, the accessor protocol is a powerful abstraction which is not only performant, but can accommodate new use cases with minimal effort.

Conclusion

In this post, we dove deep into techniques for array-like object iteration. Along the way, we discussed the limitations of current approaches and identified opportunities for a lightweight means for element retrieval that can flexibly accommodate a variety of use cases, including strided arrays, arrays supporting deferred computation, shared memory views, and sparse arrays. We then learned about the accessor protocol which provides a straightforward solution for accessing elements in a manner consistent with built-in bracket notation and having minimal performance overhead. With the power and promise of the accessor protocol firmly established, we wrapped up by showcasing a few demos of the accessor protocol in action.

In short, we covered a lot of ground, but I hope you learned a thing or two along the way. In future posts, we'll explore more applications of the accessor protocol, including in the implementation of complex number and boolean typed arrays. We hope that you'll continue to follow along as we share our insights and that you'll join us in our mission to realize a future where JavaScript and the web are preferred environments for numerical and scientific computation. 🚀

Athan Reines is a software engineer at Quansight and core developer of stdlib.

stdlib is an open source software project dedicated to providing a comprehensive suite of robust, high-performance libraries to accelerate your project's development and give you peace of mind knowing that you're depending on expertly crafted, high-quality software.

If you've enjoyed this post, give us a star 🌟 on GitHub and consider financially supporting the project. Your contributions and continued support help ensure the project's long-term success and are greatly appreciated!

If you'd like to view the code covered in this post on GitHub, please visit the source code repository.

License

Copyright (c) 2024 Athan Reines.

Licensed under the Apache License, Version 2.0 (the "License");
you may not use this file except in compliance with the License.
You may obtain a copy of the License at

   http://www.apache.org/licenses/LICENSE-2.0

Unless required by applicable law or agreed to in writing, software
distributed under the License is distributed on an "AS IS" BASIS,
WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
See the License for the specific language governing permissions and
limitations under the License.